| XIIIth Conference on Clay Mineralogy and Petrology, Praha (1994) | Acta Universitatis Carolinae Geologica 38(1994):253-261 Editum 24.1.1996 |
S. KRUMM
Institut für Geologie
Schlossgarten 5, 91054 Erlangen, Germany,
[email protected]
| Accepted November 1, 1995 |
|
ABSTRACT: WINFIT is a public domain program designed for line-profile analysis of broad and heavily overlapping X-ray reflections that are common in clay mineral analysis. In many cases only little a priori information on the shape of these lines is available. Therefore, parameter correlation effects can cause the refinement algorithm to fail. In these instances frequent user interaction is necessary. WINFIT's user-interface allows easy access to the parameters describing a peak by dialog boxes. Individual parameters or groups can be excluded from or included in the fit by simple mouse-clicking. Crystallite size analysis is performed either on single peaks or on multiple orders of a lattice direction using a variety of methods, including Warren-Averbach algorithms. For the analysis of illite, a correction against the structure factor is implemented. |
INTRODUCTION
The exact determination of peak parameters like area and breadths from experimental diffractograms is hindered by peak overlap and noise. Especially if Fourier or variance techniques are used for determination of crystallite size and lattice strain, the exact profile of a reflection has to be known. Small amounts of remaining noise can cause failure of the analysis. Any smoothing procedure on the other hand leads to distortion of the original peak profile. A better way is to model a profile shape function (PSF) to the experimental data and calculate the variables of interest from the function parameters. WINFIT is split in two sections:
GENERAL DESCRIPTION
The program runs under Microsoft WINDOWS which offers several advantages for the user and programmer. One does not have to care about the specific hardware configuration. WINFIT can be used with any screen, printer and mouse supported by WINDOWS. The WINDOWS clipboard enables data exchange with other programs. Every screen (raw data, graphical representation of the fit, fit and crystallite size results) can be printed out, transfered to other programs (e.g. CorelDraw) or stored as a metafile. Due to the quasi multitasking capability of WINDOWS the program can be run in the background. Interaction with the user is performed by pulldown-menues and message boxes. The program makes suggestions what step should be carried out next (Fig. 1). More support can be obtained from an online help system. Data input and manipulation is done by readable dialog boxes. WINFIT reads in a variety of diffraction data file formats:
The facilities for pretreatment of the data before fitting include correction against the Lorentz-Polarisation factor, stripping of alpha2 and conversion between fixed and variable divergence slit geometry. No smoothing algorithms are provided because profile-fitting models the pattern over a much larger range than any digital filter. Additional smoothing prior to fitting is considered "redundant and may introduce significant error into the data" (Howard & Preston 1989).
FITTING SECTION
After loading a diffractogram, the user is asked to mark an angular range for fitting and to select the peaks for refinement by mouse-clicking. From this an initial approximation of the fitting parameters are made which are refined afterwards by the Levenberg-Marquardt method (Press et al. 1992).
The PSF used is a split Pearson VII function that, if requested, can be fixed to Gaussian, Lorentzian or any intermediate type. One can choose between a unique line shape for all reflections or individual shapes for each line. Decomposition of the alpha2-component of the pattern can be selected. The sattelite line is then modeled by the shape of the alpha1- line, having about half its intensity and a position calculated from that of the alpha1-peak.

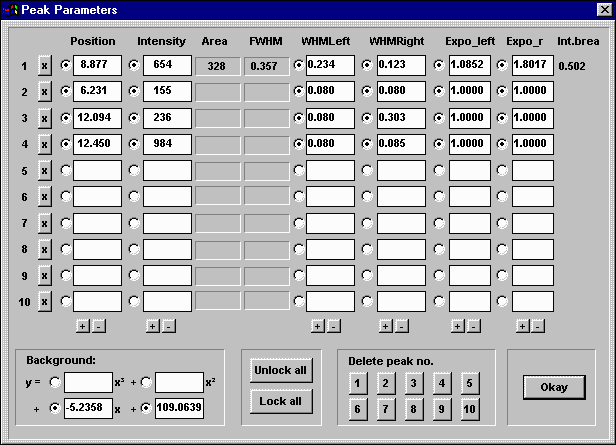
The peak parameter dialog box allows easy modification of the parameters. Individual peaks and parameters as well as groups of parameters can be excluded from the fit by just a click with the mouse (Fig. 2). The refinement can be interrupted by the user or stops after three iterations that failed to improve the fit. The background is refined by a polynomal of up to third order.The original data, the fitted reflections and the difference pattern are graphically displayed in a separate window (Fig. 3).
WINFIT calculates the commonly used criteria for goodness of fit, e.g. the reliability or residual error (compare Howard & Preston 1989), which are a measure of the squared deviation between observed and calculated intensities. If noise is present in the original data, these criteria will indicate a "poor" fit, even if the actual peak profiles are perfectly matched. To obtain additional information on how "good" the fit matches the unknown original profile, WINFIT calculates the "absolute difference" as difference between the sums of observed and calculated data divided by the sum of observed intensities. It can be assumed that random noise causes positive and negative deviations with equal likelihood. A fit of a noisy pattern with low reliability therefore may give an "absolute difference" close to zero and indicate a perfect fit.

CRYSTALLITE SIZE SECTION
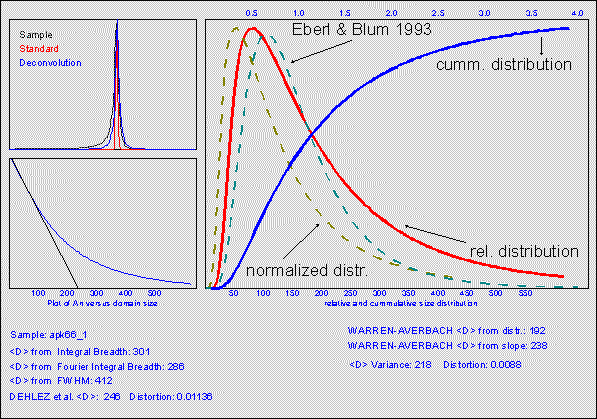
The refined peak shape parameters are used for the calculation of crystallite size and lattice strain by various single line methods and multi-order procedures. Methods based on FWHM and integral breadths are described in detail among others by Williamson & Hall (1953), Klug & Alexander (1974) and Ziegler (1981). WINFIT utilises the single line variance approach of Toth (1979) and Arkai & Toth (1983). Additionally, a procedure for separation of size and strain proposed by Dehlez et al. (1993) is available. From the Pearson exponent of the PSF the contribution of Gaussian and Lorentzian components can be calculated that are assumed to be proportional to the amount of small crystallite size broadening and strain broadening respectively. Finally, size and strain parameters are calculated by Fourier analysis. These procedures and their applicability are largely discussed in the literature (Warren & Averbach, 1950; Wagner & Aqua, 1964; Klug & Alexander, 1974; Eberl & Blum, 1993). Therefore, only the modifications and data pretreatment will be presented here.
An experimental diffraction profile [h(i)] is composed of several components. The profile related to the crystalline state of the specimen [f(i)] is broadened by convolution with the profile due to machine effects [g(i)]. Additionally, a background [backgr.] due to diffuse scattering and fluorescence is present.
h(i) = (f(i) o g(i)) + backgr.
Machine dependent broadening can be removed by Fourier-methods like the Stokes correction (Stokes 1948). The deconvolution then yields the pure diffraction profile. This itself is the product of the interference function (I) and the theta dependent functions of the polarization factor (LP) and the layer structure factor (F) (Reynolds 1989).
I(i) = I(i) * LP(i) * F(i)
If a scattering domain consist of only a few layers, the variation of F and LP with angle causes an asymmetric broadening and peak displacement, due to the large angular area over which scattering occurs (Reynolds 1989). While the Stokes method corrects for instrumental errors it does not account for the LP and G functions. This is obvious from peaks that are still rather asymmetric after the Fourier-correction.
Eberl & Blum (1993, and pers. comm.) pointed out, that the Fourier method of Warren-Averbach should be applied to the pure interference function. Therefore, the effects from the other two functions (LP and F) must be removed prior to Fourier analysis.
A correction against the LP factor is easily made by division of I by LP. Correcting against the structure factor is problematic, because its function has zero values in the range of integration. Although the peak tails fall almost to zero, division of these values by a number close to zero results in artificial spikes of high intensities.
One possibility is applying the correction after removing the instrumental contribution. As the structure factor is zero at about 10 2theta, the pure diffraction profile of eg. illite should also have zero intensities in this angular range. Any intensities observed in real patterns should be due to smearing out the f profile by the g function. However, also after applying the Fourier correction, there are still intensities that make the method fail. This is probably be due to the selection of a standard with an exceptional narrow peak breadth.
Another approach is to add a constant to every value of F thus preventing it from going to zero. Empirically a value of 500 was found to give best results. Although this value is small compared to values of 200*200 for the square of F, it causes an upward shifting of the F function. This approach is merely empirical and has no theoretical substantiation. On the other hand, it produces symmetric reflections and crystallite sizes determined on simulated profiles suggest that this method gives correct results.
The method implemented in the program uses only one half of the peak profile. The shape is calculated from the side, where F has non zero values. Then the correction against F and LP is applied and the peak is made symmetric by copying this side to the other. The justification of this method is as follows:
Another problem in determination of size-distributions by Fourier-analysis is the adoption of a specific profile shape function (Dehlez et al. 1993; Eberl, pers. communication) as it a priori influences the shape of the size distribution obtained. This is circumvented in WINFIT by the possibility of using a cluster of peaks to represent a single diffraction peak.
The procedure used for Fourier analysis
Additional features
The program does not only calculate the crystallite-size distribution (Fig. 4) and the cummulative frequency distribution, but also plots a reduced curve. This curve is obtained by dividing crystallite size by mean crystallite size and plotting this against frequency/maximum frequency. This curve can be compared to the log normal distribution described by Eberl & Blum (1993) that is characteristic for crystal growth by Ostwald ripening processes (Fig. 4). In order to evaluate the reliability of a certain crystallite-size determination method, the program offers a function to simulate a diffraction pattern for various crystallite size distributions. The pattern is calculated from the interference function, the LP-factor and the structure factor for a "normal" illite. No convolution of this pattern with the instrumental error functions are made. Therefore, in test runs the standard profile parameters must be set to very small breadths to yield correct values.
ACKNOWLEDGEMENTS
I would like to thank D.D. Eberl (USGS, Denver) for his advices and his patience in discussions on implementation of the Fourier methods. Thanks are also due to L.N. Warr (Heidelberg) for brushing up the English and helpful review on an earlier draft. WINFIT can be obtained free of charge from the author for non-commercial use.
REFERENCES
Arkai, P. & Toth, M.N. (1983): Illite crystallinity: Combined effects of domain size and lattice distortion. - Acta Geologica Hungaria, 26, 341-358.
Dehlez, R.; de Keijser T.H.; Langford, J.I.; Louer, D, Mittemeijer, E.J. & Sonneveld, E.J. (1993): Crystal imperfection broadening and peak shape in the Rietveld method. - in: Young, R.A. (ed.): The Rietveld method. - International Union of Crystallography monographs on crystallography, 5, 30-57.
Eberl, D.D. & Blum, A. (1993): Illite crystallite thickness by x-ray diffraction. - in: Reynolds, R.C. & Walker, J.R. (eds.): Computer applications to x-ray powder diffraction analysis of clay minerals. - Clay Minerals Society workshop lectures, 5, 123-153.
Howard, S.A. & Preston, K.D. (1989): Profile fitting of powder diffraction patterns. - in: Bish, D.L. & Post, J.E. (eds.): Modern powder diffraction. - Reviews in Mineralogy, 20, 217-275.
Klug, P.H. & Alexander, E.L. (1974): X-ray diffraction procedures for polycrystalline and amorphous materials. ; 966 p.
Press, W.H., Teukolsky, S.A., Vetterling, W.T. & Flannery, B.P. (1992): Numerical recipes in C - the art of scientific computing. - Second edition; Cambridge University Press, 994 p.
Reynolds, R.C. (1989): Diffraction by small and disordered crystals. - in: Bish, D.L. & Post, J.E. (eds.): Modern powder diffraction. - Reviews in Mineralogy, 20, 145-181.
Savitzky A. & Golay, M.J.E. (1964): Smoothing and differentiation of data by simplified least squares procedures. - Anal. Chem., 36, 1627-1638.
Toth, M.N. (1979): X-ray variance method to determine the domain size and lattice distortion of ground kaolinite samples. - Acta Miner. Petrogr., Szeged, 24, 115-119.
Wagner, C.N.J. & Aqua, E.N. (1964): Analysis of the broadening of powder pattern peaks from cold-worked face-centered and body-centered cubic metals. - Advances in x-ray analysis, 7, 46-65.
Williamson, G.K. & Hall, W.H. (1953): X-ray line broadening from filed aluminium and wolfram. - Acta Metallica 1, 22-31.
Ziegler, G. (1981): Charakterisierung keramischer Pulver durch ein r�ntgenographisches Messverfahren. - Keramische Zeitschrift, 33, 287-290.