Introduction
References
Package
Starting
The .dat file
The .hkl file
Output files
Strategies
Next to do
History
Bugs
GNU license
Reverse Monte Carlo and pseudo simulated annealing code for ab initio crystal structure determination, either from scratch (random starting model) or by "molecule location", fitting either to "|Fobs|" extracted by powder diffractometry or to single crystal data.
|
by chance, thanks to Monte Carlo ;-) |
 |
Last modification : July 2000
Espoir is a reverse Monte Carlo and pseudo simulated annealing code for ab initio crystal structure determination, either from "scratch" (from a completely random starting model) or by "molecule location" (analogous to the Molecule Replacement method), fitting either to the structure factors amplitudes "|Fobs|" extracted by powder diffractometry or to single crystal data (not any potential needed). This is a "last chance" program which we recommend to use only after failing with classical methods (Direct and Patterson methods).
Many molecule location programs were proposed recently (OCTOPUS, PowderSolve, ENDEAVOUR, DASH, TOPAS...), but few are easily available. Most of them are commercial and very expensive. Espoir is the only program in this category distributed with open sources (GNU Public License = GPL), and free for academic research.
The limit in the "scratch" mode seems to be close to 15-30 independent atoms maximum in the asymetric unit. This limit can be overcome by using the molecule location options in Espoir, extended to 6 independent objects (fragments and/or groups of random atoms). This version includes automatic molecule connectivity analysis and the use of torsion angles as variable parameters. The cost function depends either on "|Fobs|" extracted by powder diffractometry (or coming from crystal data), or on a pseudo powder pattern regenerated from the "|Fobs|" (maybe the unique innovation here, since Monte Carlo and simulated annealing is all old stuff).
The program was presented at EPDIC-7, Barcelona, May 2000, and the proceedings will be published in 2001 or 2002. A full preprint is available at :
Espoir in french = hope in english (something not to lose when dealing with structure determination by powder diffractometry). However, do not load too much hope in Espoir, you could be deceived. Every program, even a last chance one, has limits.
More about SDPD (Sructure Determination by Powder Diffractometry) in the SDPD Internet Course, see: http://sdpd.univ-lemans.fr/course/
To be cited in case of use :
- A. Le Bail, "ESPOIR: A program for solving structures by monte Carlo analysis of powder diffraction data," Materials Science Forum 378-381 (2001) 65-70.
Applications published using ESPOIR :
- Y. Laligant, A. Le Bail and F. Goutenoire, "Ab initio structure
determination of lanthanum cyclo-tetratungstate
alpha-La2W2O9 from X-ray and neutron powder diffraction," J.
Solid State Chem. 159 (2001) 223-227.
- R.I. Walton, F. Millange, D. O’Hare, A. Le Bail, T. Loiseau, C. Serre, G. Férey, "The room-temperature crystallisation of a one-dimensional gallium fluorophosphate, Ga(HPO4)2F.H3N(CH2)3NH3·2H2O, a precursor to three-dimensional microporous gallium fluorophosphates," Chem. Comm. 3 (2000) 203-204.
- A. Le Bail, P.W. Stephens and F. Hubert, "A crystal struicture for the souzalite/gormanite series from synchrotron powder diffraction data." submitted to European Journal of Mineralogy. the manuscript can be seen at : http://sdpd.univ-lemans.fr/souza.pdf
Please send references to [email protected]
if you publish an applicatiuon using ESPOIR - thanks.
This ESPOIR 3.5 package, espoir.zip contains :
- espoir.exe : ESPOIR 3.0, executable for Win95/98/NT
- espoir.hlp : The Windows Help file
- espoir.cnt : The content by topics of the Help file
- prespoir.exe : This program may help you to prepare the .dat file
- template.dat : Alternative to the prespoir.exe use for preparing a .dat file
- examples.zip : Example files
- rasmol.exe : RASMOL (by Roger Sayle) companion program for drawing .xyz files
- raswin.hlp : The RASMOL Windows Help file
- rasmol.hlp : The RASMOL help for the command line
Unzip all these files in any directory
named at your convenience, and run the program (no DLL needed, nothing
to change in the autoexec.bat file...).
The source code
The source codes ready for compilation by both MS Visual C++6 and Compaq Visual Fortran 6.1 running under MS Visual Studio 6.can be found at :
If you wish to build a DOS/UNIX/LINUX version without any GUI, you will find the Fortran source code ready for compilation by Compaq Visual Fortran 6.1 at :
This version possess exactly the same functionalities
as the Windows version.
For each of them are given 2 files, the name.dat containing instructions and the name.hkl containing reflections :
generic file
name
Scratch files (independent atoms only)
al2o3 : Al2O3 in R-3c
cuvo3c : CuVO3 in P -1
Molecule location files
zhucl : 2 objects : a CoN5O octahedron and a Cl atom
tetrasync: tetracycline hydrochloride (SDPDRR) : two objects
ibuprofen: ibuprofen : one object, 4 torsion angles
zhutest2 : 2 objects : a CoN5O octahedron and a NO3 molecule
zhutest3 : 3 objects : like zhutest3 plus an independent O atom
Two files are absolutely necessary for running Espoir :
1. name.hkl containing the "|Fobs|", from any origin (powder data or single crystal). Be careful : never enter any intensity in that program : exclusively structure factor amplitudes (corresponding to HKLF 3 card for SHELX users)
2. name.dat containing parameters defining the model (scratch or molecule fragment) and piloting the Monte carlo process (it is like trying to pilot a bottle in the ocean : you just can hope to attain your expected destination, but Espoir will sometimes guide you somewhere that you may not have expected).
Recommendations for preparing a new .dat file are to copy one of the example files, rename it, adapt it to your needs. Other possibility is to open template.dat, save it under another name, and fill in the blank lines. Finally, you may use the prespoir program delivered with the package.
Recommendations for preparing a .hkl file
are to record a good powder diffraction pattern (no preferred orientation),
then, having determined the cell and the space group, to extract the structure
factor amplitudes by using either Fullprof, WinMProf, GSAS (...) which
apply the Le Bail method, or use the Pawley method with the program of
your choice. Use then the U,V,W parameters refined during the "|Fobs|"
extraction (the Caglioti law parameters) for the regeneration of the pseudo
powder pattern in Espoir. In that way, you will avoid overlapping problems.You
may also apply Espoir to |F| single crystal data.
Running the Program
The Windows PC version will run by clicking on Espoir.exe, opening the window shown below :
Click on "File" and then on "Open file", and select your data file, for instance cuvo3C.dat from the example files.
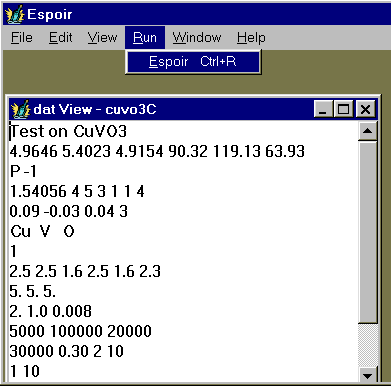
A window is open in which you may see the parameters piloting the Espoir run, modify them if you wish. In that case, you should save the file before running Espoir.
If you wish to create a new .dat file, you may "Open" the template.dat file and "Save as" it under a name of your choice. However, the best and recommended method is to copy an existing file under another name, and then to modify it. Another possibility is to use the Prespoir program which helps interactively for the .dat file creation (unfortunately, Prespoir is not yet integrated inside Espoir).
You may also edit and modify the associated cuvo3C.hkl file (changing the reflection number, for instance) before to start the Monte Carlo procedure, by clicking on "View" and then on "hkl" (the generic "name" - here cuvo3C - has not to be given since the program already knows it after the name.dat file opening). "Cut", "Copy" and "Paste" are possible by the "Edit" command.
Then start the Monte Carlo procedure by clicking on "Run", and then on "Espoir" (see above). Alternative is to use the shortcut : Ctrl+R. A new "Progress View" window is open in which details are given in text mode about the intermediate results. You will have then to wait, possibly a lot (between a few seconds and several days, depending on your problem complexity).
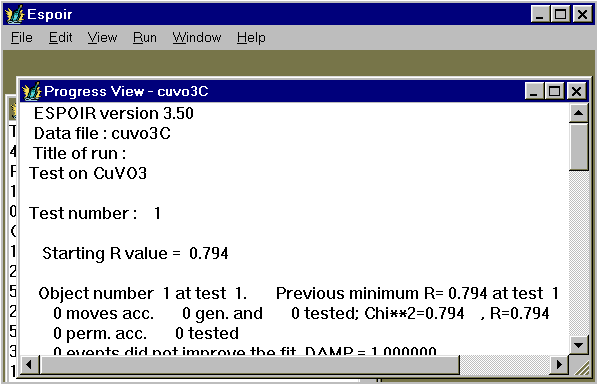
As soon as the first test is finished, access will be open to some details concerning the best test already completed by the program. Depending on the choice of the ipri parameter (see below), determining the various output files, you may either :
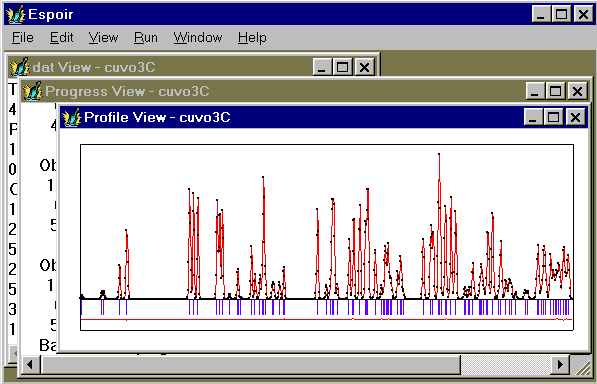
- See the regenerated observed and calculated patterns (name.prf file). For that you will have to click on "View" and then on "Profile" in order to make appear the profile drawing :
- See the final structure in different ways (WinORTEP or WinSTRUPLO by using the .ins file ; RASMOL by using the name.xyz file, clicking on "View" and then on "Structure" (see below); STRUVIR by using the namestru.dat file ; NETSCAPE or EXPLORER with a VRML viewer by using the namepo.wrl or namewi.wrl files ; PLATON by using the .spf file, etc.
Of course, in the above case, viewing an inorganic structure like CuVO3 with RASMOL is not completely satisfying... You should prefer WinStruplo or Winortep by using the .ins file.
- See the animation of the accepted Monte Carlo events (nameN.xyz), where N = the test number in that run, by using WINMOL or CHIME (see below - CHIME is built on a RASMOL basis), a plug-in for browsers like Netscape or Internet Explorer:
In that case, the .xyz file contains the whole series of coordinates stored after each accepted Monte Carlo event. Moreover, not only the atoms in the asymetric unit are shown, but also those obtained by applying the space group symmetry. See an example of such animation in the ibuprofen case.
- Etc (see the various output files and
their format in that Help file).
Why Espoir may work ?
What is the difference with a simple grid-search
program which would possibly need years for finding a solution (excepted
if the solution is at the grid beginning...)? Time is to pull down of his
pedestal the Monte Carlo and simulated annealing process in the case of
molecule location. Well, this is because being close to the ideal position
will suffice to obtain a significant lowering of the R factor. The more
"close to" is large, and faster a solution will be obtained with Espoir.
That's really all. Imagine that you explore randomly the full grid: if
you have chance, you will find an edge of the potential hole, and then
the pseudo simulated annealing process will help you to go at the hole
bottom. Making numerous tests in a run increase your chances. Not so cute.
The more unstable part of the program is the STRUPLO/STRUVIR part. You may avoid entering in that part by selecting ipri smaller or equal to 4.
Most frequent errors with Espoir are :
- Using intensities instead of structure
factor amplitudes in the .hkl file
- Using wrong order in the atomic
coordinates list
- Using delta values too small so
that the objects cannot move to the expected right position
Latest corrected bugs
- August 29, 2000 : In the nobt=0
case, the program changed the occup values to 1. This has been repaired.
Limits
1000 reflections
60 atoms per object, in the asymetric
unit
6 objects
8 different atom-types
16000 points in the regenerated pattern
50 rotatable bonds
Authors of Espoir for Windows
Copyright © 1999-2000
Marc Mileur for the Visual C++ part -
[email protected]
Armel Le Bail for the Fortran part - [email protected]
Web site : http://www.cristal.org/sdpd/espoir/
Acknowledgments
Thanks to Roger Sayle for that wonderful
public domain program : RASMOL.
More about RASMOL (and CHIME) at : http://www.umass.edu/microbio/rasmol/
Thanks to the Dupont de Nemours Company who decided to grant that project for improving Espoir version 2, on the recommendations of Richard Harlow, without any condition on source code and program availability, but the conditions of the GNU General Public License.
An example delivered with this version
(cuvo3c.dat) is detailed below :
Test on CuVO3 : text for this run 4.9646 5.4023 4.9154 90.32 119.13 63.93 : cell parameters P -1 : SG : Space group 1.54056 4 5 3 1 1 1 : wa, kxr, na, nt, nob, ns, ipri 0.09 -0.03 0.04 3 : U, V, W, Nstep optional if ns=1 Cu V O : atom type names 1 : ncon : constraint on distances 2.5 2.5 1.6 2.5 1.6 2.3 : rcut - optional if ncon=1 3. 3. 3. : delta (nt values) 2. 1.0 0.008 : anneal, sigma, reject 5000 100000 20000 : n1, n2, n3 20000 0.25 2 10 : nstart, rmax, ichi, ntest nob groups of lines, where nob = number of objects 1 10 : nobt, n4 : type of object, perm. 1 1 3 : ni : number of atoms of i-type 1.1 0 0 : bov, nocc, nspe optional lines according to nocc, nspe and nobt (here nothing)
Example of atomic coordinates given if nobt = 0 :
-0.0760 0.3091 -0.5059 1. : x,y,z,occupation number -0.6436 -0.8249 -0.7986 1. 0.3537 0.6792 0.6986 1. 0.9300 -0.1930 0.9905 1. -0.1040 -0.0487 -0.3215 1. : care to make a return here
Example of atomic coordinates given if nobt = 2 :
10. 10. 10. 90. 90. 90. : cell containing the fragment -0.0760 0.3091 -0.5059 1. : x,y,z,occupation number -0.6436 -0.8249 -0.7986 1. 0.3537 0.6792 0.6986 1. 0.9300 -0.1930 0.9905 1. -0.1040 -0.0487 -0.3215 1. : care to make a return hereIf the fragment coordinates are Cartesian, the cell parameters should be 0. 0. 0. 90. 90. 90.
See the example files for some combinations of objects.
WARNING about coordinates : note that the atomic coordinates should be given in the exact order defined by the ni values. For instance, in the CuVO3 case above, giving 1 1 3 as ni values, after having defined that the atom-types will appear in the order Cu V O, means that the coordinates will correspond to 1 Cu, then 1 V and then 3 O atoms, strictly in that order.
Parameter definitions
Be careful that a line
length should not exceed 80 characters
You may add comment lines
starting by character ! at column 1,
see the template.dat
file
text (format 20A4) A title for the run.
cell
(free format, 6 real).
The cell parameters a, b, c, alpha, beta, gamma
SG
The space group to be interpreted by Prof. Burzlaff's
subroutine. In principle, any SG (with inversion center at the
origin) should work.
Examples (use blanks appropriately) :
P 1 P -1 P 21/C
P 21/N C 2/M ...
P MMM P N M A
I M 2 M F M M M
C M C M
I 41/A I 4/M M M
...
P 63/M M M R -3 C P 3 2 1
...
I M 3 P -4
3 M I M 3 M
F D 3 M etc
Verify the printed symmetry operators (24 maximum, since
adding atoms due to F and I Bravais lattices has no influence
on intensity, and inversion center is treated apart).
wa, kxr,
na, nt, nob, ns, ipri
One real and 6 integers (free format)
wa
= Wavelength, only the following ones are recognized for
delta-f and delta-f" anomalous dispersion terms for
X-ray :
2.28962 1.93597 1.54051 0.70926 0.556363
kxr
= Allows to define neutron data (kxr=0)
or X-ray data (kxr=4)
na
= Total number of atoms (max = 360) in the asymetric
unit
nt
= Number of different atom types (max = 8)
If nt is negative, the scattering factors should be given
as below :
57 2000. 1.
N, X, Y
0.000 1.00000
22.599 0.95840 N
= number of couples of
45.198 0.83990
X*sintheta/lambda
67.797 0.66190
and (scattering factors)/Y.
etc
See the c60.dat example
nob
= Number of different objects (6 max). An object can be
either a rigid fragment or a group of independent atoms
ns
= Code defining the job type according to data
ns = 0 for working on "|Fobs|" (they must be quite
good, without too much overlapping) or single
crystal data
ns = 1 for working on the regenerated powder pattern
(overlapping no matter), note that the profile
shapes are Gaussian but this is not so
important, the trick is to treat overlapped data
as overlapped data, no more ;-)
ipri
= code for printing Iobs/Icalc and Fobs/Fcalc at the end of a run
if = 0 : only the name.imp file is printed out
if = 1 : like ipri = 0 plus output of the .ins and .spf files
if = 2 : like ipri = 1 plus output of the .prf and .hgl files
if = 3 : like ipri = 2 plus output of the .xyz file
if = 4 : like ipri = 3 plus output of the N.xyz files for
seing animations of the accepted Monte Carlo
events by CHIME or WINMOL
plus namestru.dat : file ready for STRUVIR
if = 5 : like ipri = 4 plus output of some other files :
- namestru.imp : distance and angles calculations
- namestru.hgl : HPGL file of the STRUVIR plot
- namestru.ps : Postscript file of the STRUVIR plot
- namepo.wrl : STRUVIR polyhedral VRML file
- namewi.wrl : STRUVIR wireframe VRML file
- namewi.pov : file for PovRay
Note that if you insert a rigid fragment inside your model (nobt=2 or 3),
you will not have access to ipri larger than 4 because of some unstabilities
in this part of the program based on STRUPLO/STRUVIR. Anyway, there
are usually no interesting polyhedron in those molecules, and the
STRUPLOprogram is made for inorganic compounds.
U, V, W, nstep
Optional line occuring only if ns = 1 (see above)
U,
V, W = Caglioti law refined when the "|Fobs|" were extracted
nstep
=
number of points that you estimate useful above the
FWHM (try nstep = 3 to 5), if nstep is given smaller that
3, it
will be reset to 3.
name1, name2...
(characters in format 8A4 )
n atom names where n = nt
In principle, ionic definitions are recognized
like O-2, Al+3, Ca+2, F-1, Ba+2, etc. (max =8)
ncon
code for constraints on shortest interatomic distances
if = 1 : read rcut below
if = 0 : no constraints
Care that there could be one optional line here :
rcut
[(nt+1)*nt/2] reals in free format
= shortest interatomic distances given in the order
11, 12, 13, 22, 23, 33 for 3 different atom types, for instance.
Note that this option of minimal distance constraints should be used with caution. It is very efficient in P1. But imagine that, in any other space group, you work with more than one object : at the beginning, all objects are misplaced, and you will refuse a move because an object hurts a misplaced object...
When Espoir checks distances for an object,
it will behave differently if the object is a rigid fragment or if it is
a group of independent atoms :
- for a rigid fragment, only the
intermolecular distances (no intra molecular ones) will be checked as anti
bumping.
- for independent atoms, all interatomic
distances are checked
This means that you may have advantage to introduce several times the same atom type, aif it can belong to both a fragment and a group of independent atoms. This will allow you to play with two kinds of distances involving this atom type.
delta1, delta2...
(reals)
The maximum move for each type of atom.
Recommended values are in the range 0.1-0.5 in the final stages.
Use values of the order of 5 Angstroms at the beginning (or more,
up to the cell parameters). Otherwise, you may stick to a false
minima. A value of zero is possible and will allow only some types
of atoms to move. Delta values are progressively damped by the
anneal parameter below.
A rigid object will be translated by the average of the delta values
of the atoms in that object. If no atom can move in an object, that
object will not move at all (no rotation, no translation).
anneal, sigma,
reject (reals)
anneal
: Move amplitudes will be progressively reduced following the
equation :
move=move*dump
dump=(1.-ngent/ngenmax*nob)**anneal
ngent = number of generated events during the program run
ngenmax = maximum number of events allowed (see n2).
For anneal=1, the move amplitude reduction will be linear.
It is suggested to use nanneal=2.
Note that dump will apply on atom moves but also on molecule
translations if Rp(F) or RF < rmax (see rmax definition below).
Note that damp will apply on atom moves but also on molecule
translations. Damp will apply to rotation angles of the global molecule
and/or to torsion angles only after damp < 0.5.
This
is a way for doing some simulated annealing, avoiding sometimes
the necessity to make two steps (one step with large move
amplitudes, and a subsequent step with smaller move amplitudes)
sigma
= standard deviation on |F| (an overall value).
The best is to explore different values. Data are arbitrarily
normalized for having a mean |F|=50. You may try sigma=1.
to sigma = 0.1 or 0.01 and see the result.
This parameter is of no use if you select ichi=2 below.
reject
= test for accepting randomly 40% moves that do not improve
the fit. Anyway, all events that lead to delta(R) < -reject are
really rejected, where R is the reliability on |F|
Try reject = 0.01 or 0.005, and observe the number of kept events.
Remember that a global decrease of R is searched, so that reduce
reject if R does not finally decreases.
This could help in not being trapped in a false minima.
The value of reject is dumped by the anneal parameter (see
above), progressively reduced to zero up to n2 (see below), the
total number of events, is reached.
n1, n2, n3
(3 integers)
n1
: Determines how often a summary will be written to the standard
output. It will be every after n1 events generated (moves +
permutations) except that it will only occur when an event is
accepted.
n2
= The total number of events the program should run for.
n3
= The number of events afterward the results will be saved
(possibly several times in a run).
nstart, rmax,
ichi, ntest
If after
nstart
(integer) events (moves + permutations), the R factor is
still higher
than rmax (real), then restart from a new random
configuration,
unless the total number of runs (ntest) is already
attained.
ichi
(integer) determines the test made for accepting or rejecting an
event :
ichi = 1 : the test is made on the decreasing of
Sum on (|Fobs|-|Fcalc|)**2/sigma**2
ichi = 2 : the test is made on the decreasing of R :
Sum on | |Fobs|-|Fcalc| | / Sum on |Fobs|
Try both, however, there seems to be no clear difference.
Recommended values :
nstart = 40000 and
rmax
= 0.2 - 0.3 is fine for small structures in scratch
mode.
nstart = 120000 and
rmax
= 0.35 -0.40 could work for large structures
The group of following
lines have to be given nob times,
where nob is the number of objects.
nobt, n4
2 integers
nobt
= giving the type of that object
nobt = 0 : group of independent atoms at known
starting coordinates
nobt = 1 : group of independent atoms introduced
randomly
nobt = 2 : rigid fragment
nobt = -2 : rigid fragment and you want to play with the
maximum rotation angle (normally 360°).
Then an optional line has to be given after
the [nobt, n4] line, which should be the
maximum rotation angle in (°) for the whole object.
nobt = 3 : fragment with free torsion angles
nobt = -3 : fragment with free torsion angles and you want
to play with the maximum rotation angles (normally 360°).
Then an optional line has to be given after
the [nobt, n4] line, with 2 angles :
The maximum rotation angle in (°) for the whole object.
And the maximum rotation angle in (°) for the torsion angles
n4
: this parameter may have 2 meanings according to the
nobt values :
if nobt = 0 or 1 : try permutations of atoms after n4
moves. Examples :
If n4 = 10, the ratio of atom moves and
permutations will be 10 for 1.
If n4 = 1, only permutations will occur
If n4 = 0 only atom moves will occur
care that some combinations of constrained
occupation numbers may not allow any
permutations. If permutations are not allowed, the
program will infinitely loop, but you will be given a
message ;-).
Try n4=10 to 100 like you wish (most test files use
n4=10)
if nobt = 2 : try translations of model after n4 rotations
If n4 = 10, the ratio of rotations and translations will
be 10 for 1.
If n4 = 1, only translations will occur (not
recommended in the general case)
If n4 = 0 only model rotations will occur (not
recommended as well)
Rotations are made around the molecule (or
fragment) center of gravity.
Try n4 = 2 to 25 or more if you wish (many test files
use n4=2 or 4 when nobt = 2)
If torsion angles and global molecule rotation can both occur, then this
is
done by a random approach : either torsion angle or global rotation at
50%
chances, then if the Monte Carlo event is to change a torsion angle value,
the torsion angle to be modified will also be chosen at random among all
possible torsion angles. If you have better ideas, tell us...
ni1, ni2...
nt values (integers)
ni
= numbers of atoms in each type in the object
in the same order as their names above (integers in free
format). Some ni values can be zero.
(sum of ni values is max 50 for one object, 200 for 4 objects)
bov, nocc, nspe
: one real and 2 integers (free format)
bov
= Overall thermal B factor (real in free format)
Use a value near of 1.0 or 1.5 for inorganic materials
and 3.0 or more for organic compounds.
nocc
= code for reading individual guessed occupation factors
if = 1 : a next optional line should give all the occup. factors
if = 0 : the program generates all occup = 1.
nspe
= code for general or special positions
if = 1 : read special positions codes nsp below
if = 0 : all atoms in general position, do not read anything
Of course, if nocc=1 and nspe=1, then 2 optional lines should be given next, in that same order.
And the special position codes (nsp) currently defined in the program are :
nsp code position nspe code position 1 - x,y,z general position 2 - x,x,x 6 - x,0,z 9 - x,y,0 10- 0,y,z 13- x,0,0 12- 0,y,0 8 - 0,0,z 3 - 0,0,0 14- 1/2,0,0 15- 0,1/2,0 16- 0,0,1/2 17- 1/2,1/2,1/2 18- 1/2,1/2,0 19- 1/2,0,1/2 20- 0,1/2,1/2 21- x,1/2,1/2 22- 1/2,y,1/2 23- 1/2,1/2,z 24- x,0,1/2 25- 0,y,1/2 26- 1/2,0,z 27- x,1/2,0 11- 1/2,y,0 5 - 0,1/2,z 28- x,1/2,z 29- 1/2,y,z 30- x,y,1/2 4 - x,1/4,z 31- x,y,1/4 32- 1/4,y,z 33- 1/4,1/4,0 34- 1/4,0,1/4 35- 0,1/4,1/4 36- 1/4,1/4,1/2 37- 1/4,1/2,1/4 38- 1/2,1/4,1/4 7 - x,0,1/4 39- x,1/4,0 40- 0,y,1/4 41- 1/4,y,0 42- 0,1/4,z 43- 1/4,0,z 44- x,1/2,1/4 45- x,1/4,1/2 46- 1/2,y,1/4 47- 1/4,y,1/2 48- 1/2,1/4,z 49- 1/4,1/2,z 50- x,1/4,1/4 51- 1/4,y,1/4 52- 1/4,1/4,z 53- 1/4,1/4,1/4 55- 3/4,3/4,3/4 56- x,1/4,3/4 57- x,3/4,1/4 58- 1/4,y,3/4 59- 3/4,y,1/4 60- 1/4,3/4,z 61- 3/4,1/4,z 54- 1/4,1/4,3/4 62- 3/4,1/4,1/4 63- 1/4,3/4,1/4 64- 0,1/2,1/4 65- 0,1/4,1/2 66- 1/2,0,1/4 67- 1/4,0,1/2 68- 1/2,1/4,0 69- 1/4,1/2,0 70- 1/2,1/2,1/4 71- 1/2,1/4,1/2 72- 1/4,1/2,1/2 73- 1/4,0,0 74- 0,1/4,0 75- 0,0,1/4 76- 3/4,1/4,1/2 77- 1/2,3/4,1/4 78- 1/4,1/2,3/4 79- 3/4,1/2,1/4 80- 1/2,1/4,3/4 81- 1/4,3/4,1/2 82- 1/4,3/4,0 83- 0,1/4,3/4 84- 3/4,0,1/4 85- 1/4,0,3/4 86- 0,3/4,1/4 87- 3/4,1/4,0 88- 0,1/2,1/4 89- 1/4,0,1/2 90- 1/2,1/4,0 91- 0,1/4,1/2 92- 1/4,1/2,0 93- 1/2,0,1/4 94- 1/8,1/8,z 95- 1/8,y,1/8 96- x,1/8,1/8 97- 1/8,1/8,5/8 98- 1/8,1/8,1/8 99- 0,1/4,5/8 100- 0,1/4,1/8 101- x,x,0 102- x,x,1/2 103- x,x,3/8 104- x,x,5/8 105- x,x,1/4 106- x,x,3/4 107- x,x+1/2,1/4 108- x,x+1/2,1/2 109- x,x+1/2,0 110- x,x+1/2,3/4 111- x,x,z 112- x,x+1/2,z 113- x,-x+1/2,1/4 114- x,-x,z 115- x,-x,1/2 116- x,-x,0 117- x,-x,1/4 118- x,1/4,1/8 119- 1/4,y,1/8 120- x,x+1/4,7/8 121- x,x+1/4,1/8 122- 0,3/4,1/8 123- 0,1/4,3/8 124- 0,1/4,1/8 125- 1/3,2/3,z 126- 2/3,1/3,z 127- 2/3,1/3,1/2 128- 2/3,1/3,0 129- 2/3,1/3,1/4 130- 1/3,2/3,1/2 131- 1/3,2/3,0 132- 1/3,2/3,1/4 133- 1/3,2/3,3/4 134- 2/3,1/3,3/4 135- x,-x,5/6 136- x,-x,1/3 137- x,-x,1/6 138- x,-x,2/3 139- x,0,5/6 140- x,0,1/3 141- x,0,1/6 142- x,0,2/3 143- x,2x,1/4 144- x,2x,3/4 145- x,2x,1/2 146- x,2x,0 147- x,2x,z 148- x,1/8,1/8 149- 1/8,1/8,1/8 150- 5/8,5/8,5/8 151- 7/8,7/8,7/8 152- 3/8,3/8,3/8 153- 7/8,1/8,1/8 154- 1/2,y,y 155- 0,y,y 156- 1/4,y,y 157- 1/2,y,-y 158- 0,y,-y 159- 1/4,y,-y 160- 1/4,y,y+1/2 161- 1/2,y,y+1/2 162- 1/4,y,-y+1/2 163- 1/8,y,-y+1/4 164- 1/8,y,y+1/4 165- 5/8,0,1/4 166- 1/8,0,1/4 167- 7/8,0,1/4 168- 3/8,0,1/4How many atoms in general and special positions ? You have to guess !
So : care that there could be up to 2 optional
lines here :
occupation factors (real in free format)
nsp codes for special positions (integers in free format)
If you have 100 atoms, your optional lines
may extend on several lines. The important point being that the expected
number of values is found by the program.
if nobt = 1 the object is a group
of atoms with random coordinates, and
no data is given
if nobt = 0 the object will reuse
previous atomic coordinates and the
x,y,z,occup should be given just below
if nobt = 2 the object is a fragment
and
the next line should be either
a,b,c,alpha,beta,gamma
of the cell in which is described the molecule
or 0. 0. 0. 90. 90.
90. if the model is described with Cartesian
coordinates and the following
lines will then be the x,y,z,occup values as
described below
x,y,z,occup
(reals) Lines of atomic coordinates and occupation
numbers (max 50 atoms)
occup
=
1 means a general position fully occupied
Note that if nobt is different from 0, then occup will either
be always = 1 for any atom (the program cannot decide in your place), or
defined by nocc parameters.
WARNING about coordinates : note that the atomic coordinates should be given in the exact order defined by the ni values. For instance, in the CuVO3 case above, giving 1 1 3 as ni values, after having defined that the atom-types will appear in the order Cu V O, means that the coordinates will correspond to 1 Cu, then 1 V and then 3 O atoms, in that strict order.
End of nob groups of lines
See the example files for details.
The organization in the .hkl file is quite simple :
One line for the number N of hkl (N maximum is 1000), and then N lines including h, k, l, |Fobs|. An example is below. Data are not formatted, just list 3 integers and one real in free format.
A sufficient number of hkl could be 10 reflections for one atom in the asymetric unit.
120 0 1 0 21.580 you may find possibly next 0 0 1 39.622 values in the test files 1 1 0 9.749 but they are ignored 1 0 -1 29.746 1 0 0 195.923 ... ... ... 4 1 -2 128.143 3 4 0 159.884 0 3 3 142.716 3 2 1 8.925 2 -2 0 349.860 Care to make a return here.WARNING : No intensities here, only "|Fobs|" (corresponding to HKLF 3 card in SHELX).
Espoir will create several output files, depending on the ipri value. Files with (*) below are updated in a run only when a test gives best results than the previous tests :
name.imp : will contain all intermediate results
no more output file if ipri=0
name.ins (*) : will contain the best result in SHELX format. That file can be used for drawing by WinORTEP Or WinStruplo (see below Web sites for download).
name.spf (*) : will contain the best configuration ready for searching symmetry by PLATON (same Web siteas above for a Windows version)
no more output file if ipri=1
name.prf (*) : Contains the "observed" and regenerated powder patterns in a format readable by DMPLOT.
Note however that when the U and V parameters are different from 0, the step will be variable so that DMPLOT will not produce the correct angles and reflection positions.
name.hgl (*) : Contains the "observed" and regenerated powder patterns in HPGL format.
no more output file if ipri=2
name.xyz (*) : Contains the coordinates in xyz format (RASMOL, etc) There are only the asymetric unit coordinates in that file
no more output file if ipri=3
nameN.xyz : Contains the animation in xyz format (CHIME, WinMol) for the Nth test in the run (this can consume space on your hard disk !). That file contains the atomic coordinates for the Z units in the structure (you will see usually several molecules Moving.
namestru.dat (*) : Coordinates in STRUPLO/STRUVIR format
no more output file if ipri=4
additional files if ipri 5 : the
program will enter in the (rather unstable) STRUVIR part.
This will not be possible
with nobt=2 or 3 (molecule) since
STRUVIR is a program
for inorganic compounds.
namestru.imp (*) : Contains the distance
and angles calculations
namestru.hgl (*) : Contains the STRUVIR
plot in HPGL format
namestru.ps (*) : Contains theSTRUVIR
plot in Postscript format
namepo.wrl (*) : Contains the polyhedral
STRUVIR VRML file
namewi.wrl (*) : Contains the wireframe
STRUVIR VRML file
name.pov (*) : Contains the STRUVIR POVRAY
file
Some Web sites for finding the above drawing programs :
http://www.umass.edu/microbio/rasmol/
for CHIME (browser plug-in) and RASMOL
http://www.chem.gla.ac.uk/~louis/software/
for WinORTEP or WinSTRUPLO or PLATON
ftp://iris.unipress.waw.pl/pub/dmplot/
for DMPLOT
http://www.povray.org/
for POVRAY
http://www.ccl.net/cca/software/MS-WIN95-NT/index.shtml
for WINMOL
http://sdpd.univ-lemans.fr/vrml/struvir.html
for STRUVIR
http://www.cai.com/cosmo/
for Cosmo Player VRML viewer, as a browser plug-in
Lists of drawing software available at :
http://www.ccp14.ac.uk/solution/structuredrawing/index.html
http://www.claessen.net/chemistry/soft_viz_en.html
http://www.iucr.org/sincris-top/
Pure Scratch
- Al2O3
- CuVO3
Molecular Replacement
- Finding an octahedron
- One fragment and one atom
- Two fragments
- Three objects
More objects
Last words
General
Espoir needs a cell, a space group and structure factors. That means that you should have indexed the cell, guessed a space group, and either extracted the "|Fobs|" from a powder pattern by any way at your convenience (see the SDPD tutorial at http://sdpd.univ-lemans.fr/iniref/indexa.html), or recorded single crystal data. Care to the quality of your "|Fobs|". Remember that using the largest number of reflections is not a good idea with Espoir (because the large angle data do not contain that much information due to overlapping) : Give to Espoir the strict minimum of data, as defined below, no more.
Key parameters : nobt and ns.
The nobt parameter is the key for applying the chosen strategy. This parameter allows you to define the type of object(s) included in your starting model :
nobt = 1 : scratch (i.e. atoms at random
positions)
nobt = 2 : fragment or molecule to be
located by rotations/translations.
nobt = 3 : fragment or molecule with torsion
angles to be located by rotations/translations. In that case, the total
number of rotations is distributed equally, but at random, between rotations
of the global object and torsion angle rotations along the rotatable bonds
automatically located by Espoir.
And you may also use a group of independent atoms at defined positions as starting object with nobt = 0. In such a case, you can do only one test in a run.
Obtaining Cartesian coordinates for >200000 molecules is quite easy and free at http://www.molecules.com/. Otherwise, use the Cambridge Structural Database (CSD).
The other key is the ns parameter, depending on the data quality (overlap or not) :
ns = 0 : working on "|Fobs|" (they must be quite good, without too much overlapping) or single crystal data.
ns = 1 : working on the powder pattern regenerated from the "|Fobs|" (overlapping no matter), note that the profile shapes are Gaussian but this is not so important, the trick is to treat overlapping data as overlapping data, and gain on speed, no more ;-)
How many reflections ?
The first 50 "|Fobs|" were sufficient for all Molecule Replacement (MR) examples (locating one fragment corresponds to 6 degrees of freedom). Probably 30-50 "|Fobs|" would even be sufficient (and save time) for locating one fragment, and 90-150 reflections for locating 3 fragments.
Ten reflections by independent atom is the minimum for a pure scratch test. This corresponds to just more than 3 reflections per freedom degree. Giving more data may not be paying at all (longer times of calculation and program confused with high degree of overlapping data).
How many Monte Carlo events ?
For pure scratch option : 5000 to 8000000 events were used, depending on the problem complexity.
For pure Molecule Replacement : 5000 to 400000 events should be sufficient.
How many tests in a run ?
If you have not any proposition after 10 tests in a run, consider to increase to 50 or 100 tests or even more before to give up. But try also to change some important parameters in your run, and retry. Anyway, this is your last chance, since you failed with the classical methods...
How much time ? How many atoms ? How many objects ?
Well, depending on the complexity of your
problem, a few minutes to several days, months, or years (Nature needed
million years for finding the quite complex DNA structure, why would you
expect less time from Espoir ?). The more the object number and the more
the time. The more the atom number and the more the time... and the more
the number of independent runs needed (the success ratio is weaker and
weaker). In reasonable time, you may expect to solve 30 independent atoms
problems with very good data, or 200 atoms in 4 rigid-body fragments.
Pure Scratch (random independent atoms : nobt = 1)
The recommended strategy is to try with all the possible space groups (for instance, you may have a case where you should try Immm, I222, I212121, Imm2, Im2m, and I2mm), but maybe in P1 if your problem does not exceed 30 independent atoms in that space group. The problem of determining if atoms are on special or general positions is your problem : think.
In scratch mode, ESPOIR works generally better in P1 space group. If you decide to give a try in P1, you need to present the "|Fobs|" as if they were corresponding to the P1 space group, by running an extraction in P1, of course (this may need some idiot things with FULLPROF like not using exact 90° angles but 90.0001 instead, etc...). Extinctions should obviously be considered as giving |Fhkl| = 0. and therefore this is a quite useful information for ESPOIR that you should absolutely include. Of course, the "|Fobs|" quality is essential.
The starting configurations are built up by using a generator of random positions inserted in ESPOIR.
The first example (al2o3.dat) has ns=1 and so works on the pattern regenerated from the "|Fobs|", with nob=1 and nobt=1, thus working in scratch mode, with ntest=10 (10 independent runs) :
Al2O3 R-3c 4.764 4.764 13.009 90.0 90.0 120.0 R -3 C 1.54056 4 2 2 1 1 1 0.02511 -0.04562 0.03019 3 Al+3O-2 1 distance constraints 3.0 1.6 2.2 Al-Al, Al-O, O-O 6. 6. 2. 1.0 0.002 5000 20000 20000 5000 0.2 2 10 1 10 1 1 1.0 1 0 2. 3. note that the occupation numbers are givenThe final coordinates are below :
Final coordinates x,y,z and occupation numbers Al1 0.99328 0.00374 0.64793 2.000 O1 0.35634 0.32461 0.58273 3.000
Final RF factor = 5.0515663E-03 Final Rp(F) factor = 4.9818517E-03You will have to recognize that Al and O are close to special positions
Now see the .prf file by the DMPLOT software :
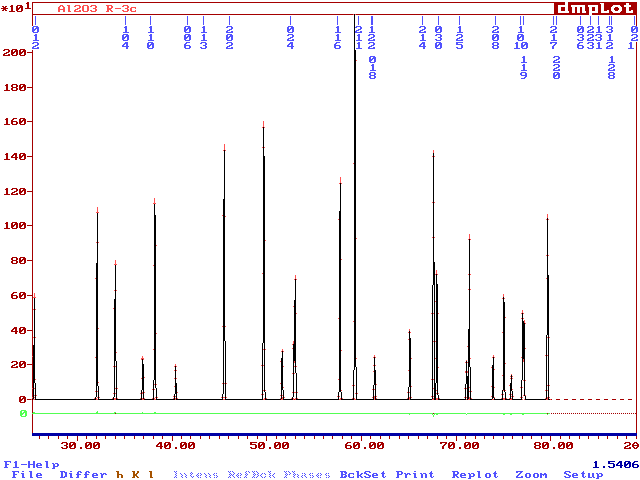
You may note that the hkl are at the good positions but the peaks are not (because the calculation is made with a variable step : indexed on the FWHM). Accordance between hkl markers and peak positions will only occur if U=V=0, giving constant FWHM related to W. So, you have seen now what is the pattern "regenerated" from the "|Fobs|". Of course, there is no relation with the true powder pattern on the point of view of peak heights. But this artifact allows to cope with overlapping peaks.
Test on CuVO3 4.9646 5.4023 4.9154 90.32 119.13 63.93 P -1 1.54056 4 5 3 1 1 1 0.09 -0.03 0.04 3 Cu V O 1 2.5 2.5 1.6 2.5 1.6 2.3 3. 3. 3. 2. 1.0 0.008 5000 100000 20000 20000 0.25 2 10 1 10 1 1 3 1.1 0 0The success is obtained for 2 runs on 10 :
Final coordinates x,y,z and occupation numbers Cu1 0.77860 0.57100 0.13880 1.000 V1 0.79130 0.06320 0.64800 1.000 O1 0.35460 0.22480 0.57170 1.000 O2 0.01120 0.76360 0.06280 1.000 O3 0.27340 0.76790 0.70730 1.000
Final RF factor = 4.8206953E-06 Final Rp(F) factor = 3.5013954E-06
Finding an octahedron
A powder pattern was calculated by using
the SDPDRR sample
I characteristics, but keeping only 2 CoN6 octahedra related by the 21
axis. Then ESPOIR 3 was run with (zhutest.dat) :
Finding an octahedron CoN6 7.662 9.626 7.072 90. 106.20 90. P 21 1.54056 4 7 2 1 1 1 0.25000 -0.26925 0.12779 3 Co N 1 5. 1.9 2.3 7. 7. 2. 1. 0.01 500 5000 5000 2000 0.20 2 10 2 2 1 6 1.5 0 0 10. 10. 10. 90. 90. 90. 0.40 0.20 0.101 1.00 0.607 0.20 0.101 1.00 0.207 0.20 0.101 1.00 0.40 0.407 0.101 1.00 0.40 -0.007 0.101 1.00 0.40 0.20 0.308 1.00 0.40 0.20 -0.106 1.00The success rate is 100% for the 10 independent runs :
Final coordinates x,y,z and occupation numbers Co1 0.50205 0.26016 0.99801 1.000 N1 0.60482 0.11379 0.21495 1.000 N2 0.40623 0.39664 0.79575 1.000 N3 0.41792 0.38063 0.19869 1.000 N4 0.58619 0.13970 0.79733 1.000 N5 0.25404 0.15864 0.92336 1.000 N6 0.75006 0.36168 0.07266 1.000
Final RF factor = 3.2756098E-02 Final Rp(F) factor = 2.3765098E-02Note that the chances to find an octahedron are enhanced by a factor 6 because of the equivalent positions which superpose the octahedron corners by 90° rotations. Thus the total number of events (rotations + translations) may be reduced to 5000 here for a full success ratio (10/10), using the 100 first reflections of the powder pattern. The final R are in the range 0.059-0.024. The original position was 0,0,0 for Co. The proposition 0.50,0.26,0.99 is correct, owing to the P21 space group (freedom along y).
- To the CoN6 octahedron above was added a Cl atom in the same cell, and the CoN6 was changed in CoN5O (zhucl.dat) :
Finding an octahedron CoN5O + Cl 7.662 9.626 7.072 90. 106.20 90. P 21 1.54056 4 8 4 2 1 1 We now have 2 objects 0.25000 -0.26925 0.12779 3 Co N O Cl 0 7. 7. 7. 7. 2. 1. 0.002 2000 60000 60000 30000 0.25 2 10 2 4 1 5 1 0 1.5 0 0 10. 10. 10. 90. 90. 90. 0.00 0.00 0.200 1.00 0.207 0.00 0.200 1.00 -0.207 0.00 0.200 1.00 0.00 0.207 0.200 1.00 0.00 -0.207 0.200 1.00 0.00 0.00 0.407 1.00 0.00 0.00 -0.007 1.00 1 0 The Cl atom is introduced here 0 0 0 1 No starting coordinates are given since nobt = 1 1.5 0 0 ESPOIR will generate the coordinates at randomThe success rate is 8/10, with the best result below :
Final coordinates x,y,z and occupation numbers Co1 0.68042 0.38060 0.06769 1.000 N1 0.60631 0.52431 0.24892 1.000 N2 0.75453 0.23690 0.88645 1.000 N3 0.42168 0.29638 0.99766 1.000 N4 0.93916 0.46483 0.13772 1.000 N5 0.76234 0.24459 0.30253 1.000 O1 0.59851 0.51662 0.83284 1.000 Cl1 0.68928 0.83174 0.51688 1.000
Object number 1 818 rot. acc. 22586 tested; Chi**2=0.958E-01, R=0.096 25 trans. acc. 7528 tested 651 events did not improved the fit, DUMP = 0.000014 Object number 2 21 moves acc. 29885 tested; Chi**2=0.958E-01, R=0.096 0 perm. acc. 0 tested 3 events did not improved the fit, DUMP = 0.000015For one atom, no permutation is allowed, of course
Tetracycline Hydrochloride : 2 objects and 2 torsion angles
With the tetracycline hydrochloride SDPDRR
data, the success rate is 2/10. There are 32 atoms in the fragment and
one independent Cl atom to find (tetrasync.dat). Espoir finds 2 torsion
angles in the starting model found in the Cambridge Structural Database
(CSD), using tetracycline hexahydrate, removing the water molecules. Two
object are entered, the C22H25N2O8 fragment and the Cl atom apart :
Test on tetracycline hydrochloride C22H25ClN2O8 synchrotron TETCYH10 10.980181 12.852233 15.733344 90.0 90.0 90.0 P 21 21 21 0.692 4 57 5 2 1 5 0.00600 0.00446 0.00257 3 C N O Cl H 0 16. 16. 16. 16. 16. 1. 1. 0.005 10000 100000 100000 30000 0.30 2 100 -3 3 360 90 22 2 8 0 24 3.5 0 0 0. 0. 0. 90. 90. 90. -2.2081 -5.3245 -3.5051 1.00 -2.7849 -6.6194 -3.7186 1.00 -4.1052 -6.9479 -3.1734 1.00 -2.0611 -7.5874 -4.4949 1.00 -0.5317 -7.5703 -4.3833 1.00 -0.0174 -7.6502 -6.8536 1.00 1.4454 -8.7923 -5.2443 1.00 0.1312 -6.2129 -4.0945 1.00 0.7153 -6.2111 -2.6783 1.00 1.5275 -4.9490 -2.3964 1.00 1.9505 -4.8280 -0.9118 1.00 2.7360 -6.0591 -0.4888 1.00 2.7359 -3.5248 -0.7258 1.00 3.7728 -3.4364 0.1915 1.00 4.4414 -2.2175 0.3971 1.00 4.0770 -1.0912 -0.3139 1.00 3.0356 -1.1522 -1.2295 1.00 2.3606 -2.3711 -1.4507 1.00 1.2660 -2.4238 -2.4374 1.00 0.7787 -3.7109 -2.8573 1.00 -0.2680 -3.7653 -3.7392 1.00 -0.8748 -5.0566 -4.2679 1.00 -4.4952 -8.2301 -3.2213 1.00 0.0533 -8.3355 -5.5292 1.00 -2.6825 -4.4164 -2.8126 1.00 -4.8680 -6.0976 -2.6366 1.00 -2.5540 -8.5358 -5.1172 1.00 0.7413 -4.7422 -0.1185 1.00 2.7169 -0.0178 -1.9072 1.00 0.7709 -1.3458 -2.8894 1.00 -0.8530 -2.6761 -4.2377 1.00 -1.2576 -4.8989 -5.6368 1.00 -5.3014 -8.4426 -2.8154 1.00 -4.0991 -8.7431 -3.5645 1.00 -0.3867 -8.1475 -3.6288 1.00 -0.4225 -9.1639 -5.6825 1.00 0.1572 -8.3942 -7.5170 1.00 1.0528 -6.9473 -6.8413 1.00 -0.9262 -7.3135 -7.0418 1.00 1.7365 -9.4734 -5.9562 1.00 2.0100 -8.0104 -5.1918 1.00 1.4350 -9.2798 -4.3841 1.00 0.8051 -6.0422 -4.7347 1.00 1.2316 -7.0575 -2.5956 1.00 -0.0508 -6.2538 -2.0928 1.00 2.2736 -5.1030 -2.8545 1.00 0.9537 -4.8415 0.5794 1.00 2.9144 -6.0295 0.4128 1.00 3.5039 -6.1533 -1.0227 1.00 2.2024 -6.8721 -0.6586 1.00 4.0558 -4.1710 0.6952 1.00 5.0732 -2.2248 1.0565 1.00 4.5374 -0.3213 -0.2192 1.00 1.9830 -0.2015 -2.2820 1.00 -0.4363 -2.0515 -3.9521 1.00 -0.5760 -4.7370 -6.0482 1.00 1 0 <-- here is entered the object number 2 : the Cl atom 0 0 0 1 0 3.5 0 0
The best model find up to now gave
R = 16.1 % on the 50 first reflections extracted from the SDPDRR synchrotron
powder diffraction data. Note that without the Cl atom, R = 37 % in that
case !
ibuprofen : one object and 4 torsion angles
In that case, one object is the molecule found at the WebMolecules Web site http://www.molecules.com/ with 4 torsion angles as located automatically by the Espoir program. The structure factors amplitudes were extracted from a routine powder pattern recorded on a STOE diffractometer (sum of 2 patterns counted one second per point, thanks to Jeremy Cockroft - that pattern being part ot the Powder Diffraction Internet Course of the Birkbeck College, London, http://pd.cryst.bbk.ac.uk/pd/). This may show that it is even possible to determine structures from low resolution and low statistics data by Espoir. Using the extracted "|Fobs|", and applying the refined structures found at CSD, one obtains, using the first 50 reflections :
IBPRAC starting model : R = 14.4
% End of Espoir moves : R = 12.6 %
IBPRAC01 starting model : R = 18.6
% End of Espoir moves : R = 14.3 %
This may be compared to R = 14,4%, the
lowest minimum found by using Espoir with the Cartesian coordinates found
at the WebMoleciules Web site :
Test on ibuprofen - pattern 2 sec from
J. Cockcroft
14.631146 7.867393
10.720177 90.000000 99.276245 90.000000
P 21/C
1.54056 4 33 3 1 1 5
0.02651 -0.04407 0.03279
3
C H O
0
14. 14. 14.
1.5 1. 0.02
10000 100000 100000
50000 0.40 2 100
-3 4
<---- nobt = -3 means that torsion angles will be varied
360 90
and that max angles are given in the line just below nobt
13 18 2
4.5 0 0
0. 0. 0. 90. 90. 90.
4.193
-0.444 -0.496 1.000
3.264
-1.041 1.795 1.000
3.189
-0.084 0.576 1.000
-3.352
0.050 0.751 1.000
-4.680
-0.656 -1.299 1.000
-3.271
-0.625 -0.643 1.000
-2.262
0.097 -1.583 1.000
1.220
-1.172 -0.627 1.000
-0.080
-1.122 -1.146 1.000
1.785
-0.044 -0.002 1.000
1.017
1.128 0.098 1.000
-0.843
0.059 -1.055 1.000
-0.283
1.181 -0.421 1.000
5.377
0.353 -1.908 1.000
3.020
-2.063 1.501 1.000
4.273
-1.025 2.214 1.000
2.560
-0.716 2.564 1.000
3.451
0.913 0.939 1.000
-4.098
-0.459 1.364 1.000
-2.390
-0.016 1.257 1.000
-3.633
1.097 0.648 1.000
-4.626
-1.166 -2.265 1.000
-5.376
-1.197 -0.658 1.000
-5.049
0.353 -1.452 1.000
-2.943
-1.659 -0.505 1.000
-2.571
1.134 -1.724 1.000
-2.274
-0.391 -2.565 1.000
1.767
-2.066 -0.705 1.000
-0.487
-1.975 -1.605 1.000
1.414
1.981 0.570 1.000
-0.840
2.066 -0.330 1.000
4.552
-1.606 -0.671 1.000
4.736
0.541 -1.246 1.000
You may see the animation of the accepted Monte Carlo events if you possess CHIME as a plug-in to Netscape or Internet Explorer. Click on ibuprofen12.xyz. But be prepared to wait, since that file contains 268 frames and weights 1468 Ko...
In that case, a NO3 molecule was inserted together with the CoN5O octahedron of the zhutest case. We have thus now to cope with two objects being independent molecules (zhutest2.dat) :
Finding an octahedron CoN5O + NO3 7.662 9.626 7.072 90. 106.20 90. P 21 1.54056 4 11 3 2 1 1 0.25000 -0.26925 0.12779 3 Co N O 0 7. 7. 7. 2. 1. 0.002 20000 200000 100000 100000 0.25 2 20 2 4 1 5 1 1.5 0 0 10. 10. 10. 90. 90. 90. 0.40 0.10 0.200 1.00 0.607 0.10 0.200 1.00 0.207 0.10 0.200 1.00 0.40 0.307 0.200 1.00 0.40 -0.107 0.200 1.00 0.40 0.10 0.407 1.00 0.40 0.10 -0.007 1.00 2 4 0 1 3 1.5 0 0 10. 10. 10. 90. 90. 120. 0.20 0.30 0.30 1.00 0.330 0.30 0.30 1.00 0.200 0.430 0.30 1.00 0.070 0.170 0.30 1.0020 runs were made and and the best result presents R~10%. 11 runs show R < 15% which are probably good as well. The best result is below :
Object number 1 at test 1. Previous minimum R=1.000 48 rot. acc. 75337 tested; Chi**2=0.103 , R=0.103 15 trans. acc. 25112 tested 28 events did not improved the fit, DUMP = 0.000020 Object number 2 at test 1. Previous minimum R=1.000 82 rot. acc. 74663 tested; Chi**2=0.103 , R=0.103 16 trans. acc. 24887 tested 61 events did not improved the fit, DUMP = 0.000020 Final coordinates x,y,z and occupation numbers Co1 0.19159 0.41337 0.07653 1.000 N1 -0.06736 0.32937 0.00221 1.000 N2 0.43303 0.49169 0.14583 1.000 N3 0.25857 0.29873 0.33441 1.000 N4 0.12461 0.52801 -0.18135 1.000 N5 0.10439 0.57476 0.22103 1.000 O1 0.27879 0.25198 -0.06797 1.000 N1 0.82494 0.33617 0.44968 1.000 O1 0.83580 0.45169 0.35841 1.000 O2 0.66711 0.28066 0.43540 1.000 O3 0.97191 0.27617 0.55523 1.000Three objects
In that case, an oxygen atom supposed to belong to a H2O molecule was added to the previous zhutest2.dat example. We have thus now to cope with three objects (zhutest3.dat) :
Finding an octahedron CoN6 + NO3 + H2O 7.662 9.626 7.072 90. 106.20 90. P 21 1.54056 4 12 3 3 1 1 0.25000 -0.26925 0.12779 3 Co N O 0 7. 7. 7. 2. 1. 0.002 2000 300000 100000 100000 0.25 2 20 2 4 1 5 1 1.5 0 0 10. 10. 10. 90. 90. 90. 0.00 0.00 0.200 1.00 0.207 0.00 0.200 1.00 -0.207 0.00 0.200 1.00 0.00 0.207 0.200 1.00 0.00 -0.207 0.200 1.00 0.00 0.00 0.407 1.00 0.00 0.00 -0.007 1.00 2 4 0 1 3 1.5 0 0 10. 10. 10. 90. 90. 120. 0.20 0.30 0.40 1.00 0.330 0.30 0.40 1.00 0.200 0.430 0.40 1.00 0.070 0.170 0.40 1.00 1 0 <-- third object 0 0 1 1.5 0 0And the best result is :
Object number 1 at test 3. Previous minimum R=0.172 189 rot. acc. 74955 tested; Chi**2=0.135 , R=0.135 9 trans. acc. 24984 tested 159 events did not improved the fit, DUMP = 0.000000 Object number 2 at test 3. Previous minimum R=0.172 171 rot. acc. 75107 tested; Chi**2=0.135 , R=0.135 8 trans. acc. 25035 tested 137 events did not improved the fit, DUMP = 0.000002 Object number 3 at test 3. Previous minimum R=0.172 24 moves acc. 99918 tested; Chi**2=0.135 , R=0.135 0 perm. acc. 0 tested 5 events did not improved the fit, DUMP = 0.000001 Final coordinates x,y,z and occupation numbers Co1 0.19412 0.53563 0.06463 1.000 N1 0.14626 0.67733 0.26467 1.000 N2 0.24197 0.39394 -0.13540 1.000 N3 -0.05527 0.44380 0.04147 1.000 N4 0.44350 0.62747 0.08780 1.000 N5 0.31518 0.40247 0.29345 1.000 O1 0.07306 0.66880 -0.16418 1.000 N1 0.81021 0.46793 0.42364 1.000 O1 0.65144 0.45701 0.45491 1.000 O2 0.91548 0.35985 0.44297 1.000 O3 0.86373 0.58692 0.37302 1.000 O1 0.42695 0.65672 0.59874 1.000
Final RF factor = 0.3239980 Final Rp(F) factor = 0.1352600
The limit is 6 objects inside ESPOIR 3.00.
More than 6 objects can be managed possibly
by changing the array dimension parameter N_O in esp0.inc :
C Dimensions can be adapted to the available memory by changing C the values in PARAMETER statements C C N_HKL Maximum number of reflections (1000) C N_T Maximum number of different type of atom (8) C N_A Maximum number of atoms per object (60) C N_O Maximum number of different objects (6) C An object can be either : C - a rigid molecule containing up to N_A atoms C - up to N_A independent atoms C N_PTS Maximum number of points on the regenerated profile C (16000) C C Integer*4 N_HKL,N_T,N_A,N_AT,N_O,N_PTS C C Usual Parameters for PC, 64 Mbytes core memory C PARAMETER(N_HKL=1000,N_T=8,N_A=60,N_O=6,N_PTS=16000) CLast words
You may try to modify/improve ESPOIR in order to include the possibility to treat torsion angles. If you do so, please contact me, and remember, you should absolutely let the source code open (GNU license).
In the "scratch" option, ESPOIR uses the "brute force", thanks to fast and cheap computers. Is it really more capable to solve your structure than by classical Patterson and Direct methods ? This is not so sure. Have also a look at the more conventional methods as described in the SDPD tutorial. More generally, visit the SDPD Database, and subscribe to the SDPD Mailing List. Eventually, follow the SDPD Internet Course.
To be done soon (?) for version 3.5.
Want to do it ? Get the Fortran source code and compile it under Linux. Use FTNCHECK before in order to clean up the code. Change some compiler-dependent routine (date, hour, the random number generator RAN, etc).
- Add the possibility to treat torsion
angles along a cone instead of a fixed bond.
- Improve the Monte Carlo / simulated
annealing algorithm
- Add genetic algorithm possibilities
- Add viewing of the accepted Monte Carlo
events inside the program. This is now possible externally by using the
CHIME plug-in with a browser (or WINMOL), loading the nameN.xyz files.
- Finish the structure factor amplitude
plot with scales.
- Add shortcut buttons for "Run"+"Espoir"
and "Edit"+"Copy", "Edit+Paste", "Edit"+'Cut", "View"+"Profile", "View"+"Structure",
etc.
- Add "Run"+"Netscape" to see directly
the VRML file output by the CosmoPlayer plug-in.
- Add "Run"+"WinOrtep" to see directly
the structure drawing through the .ins output file.
- Add "Run"+"WinStruplo" to see directly
the structure drawing through the .ins output file.
- Add "Run"+"WinPlaton" to make directly
structure analysis through the .spf output file.
- Add "Run"+"PovRay" to see directly the
structure drawing through the .pov output file.
- Etc, etc, etc, etc.
If you want to help, or do the whole job, you are welcome !
Anyway, for the cost, you already have something...
You may consider building a version for your own computer if you possess a Fortran compiler. The source code is available. Moreover, the GNU license allows you to hack the code at your convenience. You may even modify the graphical user interface (GUI) made with the MS Visual C++ 6 compiler, running under MS Visual Studio 6 (together with the Compaq Visual Fortran 6.1 compiler).
ESPOIR 0.9
The main modifications in ESPOIR 0.9 from
the original RMCA code consisted in adding the |F| calculations for working
on crystalline compounds instead of glasses, and the possibility to permute
atoms.
MODIFICATIONS IN ESPOIR 1.0
The main modification since the first
ESPOIR 0.9 version,
is
the possibility to work with any space group, not only P1. Moreover, the
contrainsts on distances and coordination numbers were found useless and
suppressed (with or without those constraints, the retained atom moves
are almost the same), leading to computer time saving. Some simulated annealing
was introduced, progressively reducing the distances the atoms can move.
The possibility to accept events that do not improve the fit was introduced,
annealed too. When facing obviously false minima with the structure model
frozen at high R factor, the calculation automatically restarts from a
different random configuration, according to parameters selected by the
user. Many simple and understandable parameters were added that allow the
user to control more closely the way ESPOIR is working. Optimization of
the |F| calculation was done by keeping the whole stuff in memory and changing
only the arrays parts concerned by the particular moving atom or the pair
of atoms permuting.
MODIFICATIONS IN ESPOIR 2.0
Two main modifications concern :
- Fit possible on a pseudo powder
pattern regenerated from the extracted "|Fobs|" - this allows keeping the
whole set of extracted structure factors, and speed is enhanced if compared
to a fit on the true pattern. Moreover, the step is variable : indexed
on the FWHM. An output in .prf readable by DMPLOT is built (however, it
will be fully operational only if the step is constant, of course : use
U=V=0 in the Caglioti law).
- Molecular replacement method by
rotation + translation of (only) one fragment (molecule location). Test
files for molecular replacement are : pyrene (from X-ray data) ; 1-methylfluorene
(without C14) ; cimetidine (from synchrotron data) ; SDPDRR sample II (tetracycline
hydrochloride, test successful without considering the Cl atom) ; SDPDRR
sample I (cobalt amine, test successful by just searching for a CoN5O octahedra)
Minor modifications concern :
- Option of minimal interatomic
distances reinserted.
- Annealing law revisited.
- Special positions considered (not
all possibilities, but you have the source code, don't you ?)..
Version 2.01 allows to treat some data affected by twinning by merohedry. See the parameter ns=2.
Version 2.02 allows the use of molecule global scattering factors. This is of some interest for locating a C60 molecule with orientational disorder. See parameter nt which should be negative.
MODIFICATIONS IN ESPOIR 3.0
The possibility to cope with several independent
objects (4 maximum, but this may be increased easily by recompilation)
was added. An object is either defined as a rigid fragment or as a group
of independent atoms. This was sponsored by DuPont Central Research
and Development.
MODIFICATIONS IN ESPOIR 3.5
This is the first Windows beta version.
The GUI was built in C++ by Marc Mileur, during a 2-months stage (June-July
2000) at the end of his 3rd university year in computer science. A modified
RASMOL (Roger Sayle) version was included for structure viewing through
the .xyz file. The accepted Monte Carlo events as an animation (xyz file
format) are viewable by using CHIME. The program is now in mixed language
and highly compiler-dependent. The source codes are distributed with the
package. Modifying and recompiling the program needs the MS Visual C++
6 as well as the Compaq Visual Fortran 6.1 compilers, both working under
MS Visual Studio 6. However, the Fortran source code can still be compiled
alone with few modification for making either DOS or LINUX versions without
any graphical output inside, but with all the new file output additions
(xyz for CHIME, RASMOL or WINMOL or etc ; wrl for a VRML viewer ; *stru.dat
for STRUVIR...). Automatic analysis of the molecule connectivity was added
in version 3.5, with the possibility to locate torsion angles and to rotate
along them.
Copyright © 1999-2000 Marc Mileur & Armel Le Bail